算法基础

一、基础数据结构

1、数组/链表

前缀和数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class PrefixSum { 
    // 前缀和数组 
    private int[] prefix;
	  /* 输⼊⼀个数组，构造前缀和 */ 
    public PrefixSum(int[] nums) { 
    	// preSum[0] = 0，便于计算累加和 
        prefix = new int[nums.length + 1]; // 计算 nums 的累加和 
        for (int i = 1; i < prefix.length; i++) { 
            prefix[i] = prefix[i - 1] + nums[i - 1];
		} 
    }
    /* 查询闭区间 [left, right] 的累加和 */ 
    public int query(int left, int right) { 
          return prefix[right + 1] - 	prefix[left];
    }
}
  • [x] 303、区域和检索 - 数组不可变
  • [x] 304、⼆维区域和检索 - 矩阵不可变
  • [x] 剑指 Offer II 013. ⼆维⼦矩阵的和
  • [x] 1314、矩阵区域和
  • [x] 1352、最后K个数的乘积
  • [x] 238、除自身以外数组的乘积 双向前缀数组
  • [x] 523、连续的子数组和 （前缀和+哈希表（取余））
  • [x] 525、连续数组 （前缀和+哈希表）
  • [x] 560、和为K的子数组 （前缀和+哈希表）
  • [x] 325、和等于k的最长子数组长度
  • [x] 724、寻找数组的中心下标
  • [ ] 862、和至少为K的最短子数组
  • [ ] 918、环形子数组的最大和
  • [ ] 947、和可被 K 整除的⼦数组
  • [x] 剑指 Offer 66 - 构建乘积数组

差分数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 差分数组工具类
class Difference {
    // 差分数组
    private int[] diff;
    
    /* 输入一个初始数组，区间操作将在这个数组上进行 */
    public Difference(int[] nums) {
        assert nums.length > 0;
        diff = new int[nums.length];
        // 根据初始数组构造差分数组
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
        }
    }

    /* 给闭区间 [i, j] 增加 val（可以是负数）*/
    public void increment(int i, int j, int val) {
        diff[i] += val;
        if (j + 1 < diff.length) {
            diff[j + 1] -= val;
        }
    }

    /* 返回结果数组 */
    public int[] result() {
        int[] res = new int[diff.length];
        // 根据差分数组构造结果数组
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }
        return res;
    }
}
  • [x] 370、区间加法
  • [x] 1109、航班预订统计
  • [x] 1094、拼车

哈希数组

常数时间内删除/查找数组中的任意元素

  • [x] 380、常数时间插⼊、删除和获取随机元素

核⼼思想：

1、如果想⾼效地，等概率地随机获取元素，就要使⽤数组作为底层容器。

2、如果要保持数组元素的紧凑性，可以把待删除元素换到最后，然后 pop 掉末尾的元素，这样时间复杂度就是 O(1) 了。当然，我们需要额外的哈希表记录值到索引的映射。

双指针秒杀链表

1、合并两个有序链表

  • [x] 21、

2、单链表分解

  • [x] 86、

3、合并K个有序链表 （优先队列）

  • [x] 23、

4、单链表的倒数第k个节点

双节点，一个节点先走k步，再一起向后走n-k步

  • [x] 19、删除链表的倒数第N个节点

5、单链表的中点

快慢指针

  • [x] 876、链表的中间节点

6、判断链表是否包含环

快慢指针：一个fast指针每次走两步，一个slow指针每次走一步，如果两个指针最后能相遇，那么链表中一定存在环。如果要检测入环的第一个节点，可以把fast指向head，因为fast和slow相遇时路程正好差一倍，之后两个指针每次走一步，那么再次相遇一定就是第一次入环的节点。

7、两个链表是否相交

  • [x] 160、相交链表

链表双指针经典高频题

  • [x] 2、两数相加
  • [x] 445、两数相加 II （如果不用翻转列表就用栈来模拟）
  • [x] 67、⼆进制求和
  • [ ] 剑指 Offer II 025. 链表中的两数相加
  • [x] 141、环形链表
  • [x] 142、环形链表 II
  • [x] 160、相交链表
  • [x] 19、删除链表的倒数第 N 个结点
  • [x] 21、合并两个有序链表
  • [x] 23、合并 K 个升序链表
  • [x] 86、分隔链表
  • [x] 876、链表的中间结点
  • [ ] 剑指 Offer 25、合并两个排序的链表
  • [ ] 剑指 Offer 52、两个链表的第⼀个公共节点
  • [ ] 剑指 Offer II 021. 删除链表的倒数第 n 个结点
  • [ ] 剑指 Offer II 022. 链表中环的⼊⼝节点
  • [ ] 剑指 Offer II 023. 两个链表的第⼀个重合节点
  • [ ] 剑指 Offer II 078. 合并排序链表
  • [ ] 1305、两棵⼆叉搜索树中的所有元素
  • [ ] 264、丑数 II
  • [ ] 313、超级丑数
  • [ ] 88、合并两个有序数组
  • [ ] 97、交错字符串
  • [ ] 977、有序数组的平⽅
  • [ ] 剑指 Offer 49. 丑数
  • [ ] 剑指 Offer 18. 删除链表的节点
  • [ ] 360、有序转化数组
  • [ ] 355、设计推特
  • [ ] 373、查找和最⼩的 K 对数字
  • [ ] 378、有序矩阵中第 K ⼩的元素
  • [ ] 剑指 Offer II 061. 和最⼩的 k 个数对
  • [ ] 24、两两交换链表中的节点
  • [ ] 25、K 个⼀组翻转链表
  • [ ] 82、删除排序链表中的重复元素 II
  • [ ] 83、删除排序链表中的重复元素
  • [ ] 92、反转链表 II
  • [ ] 1650、⼆叉树的最近公共祖先 III
  • [ ] 1257、最⼩公共区域
  • [ ] 234、回⽂链表
  • [ ] 剑指 Offer II 027. 回⽂链表
  • [ ] 1201、丑数 III

双指针秒杀数组

双指针技巧主要包括左右指针和快慢指针

快慢指针

数组问题中⽐较常⻅的快慢指针技巧，是让你原地修改数组。

  • [x] 26、删除有序数组中的重复项

类似扩展（快慢指针）：

  • [x] 83、删除排序链表中的重复元素

  • [x] 27、移除元素

  • [x] 283、移动零

左右指针

1、二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1; // 注意
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

2、两数之和

  • [x] 167、两数之和

twoSum函数

1
2
3
4
5
6
7
8
9
10
11
12
int[] twoSum(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left < right){
        int sum = nums[left] + nums[right];
        if(sum == target){
            return new int[]{left, right};
        }
        if(sum > target) right--;
        else left++;
    }
    return new int[]{-1, -1};
}
  • [x] 15、三数之和
  • [x] 18、四数之和

nSum问题模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public List<List<Integer>> fourSum(int[] nums, int target) {
        Arrays.sort(nums);
        return nSum(nums, 4, 0, target);
    }

private List<List<Integer>> nSum(int[] nums, int n, int start, int target) {
    int len = nums.length;
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    if (n < 2 || len < n)
        return res;
    if (n == 2) {
        int small = start, big = len - 1;
        while (small < big) {
            int left = nums[small], right = nums[big];
            int sum = left + right;
            if (sum == target) {
                res.add(new ArrayList<Integer>(Arrays.asList(left, right)));
                while (small < big && nums[small] == left)
                    small++;
                while (small < big && nums[big] == right)
                    big--;
            } else if (sum > target) {
                while (small < big && nums[big] == right)
                    big--;
            } else if (sum < target) {
                while (small < big && nums[small] == left)
                    small++;
            }
        }
    } else {
        int i = start;
        while (i < len) {
            int now = nums[i];
            List<List<Integer>> sub = nSum(nums, n - 1, i + 1, target - now);
            for (List<Integer> s : sub) {
                s.add(now);
                res.add(s);
            }
            while (i < len && nums[i] == now)
                i++;
        }
    }
    return res;
}

3、反转数组

例：反转一个char[]数组

1
2
3
4
5
6
7
8
9
10
void reverseString(char[] s) {
    int left = 0, right = s.length - 1;
  	while (left < right){
    char temp = s[left];
    s[left] = s[right];
    s[right] = temp;
    left++;
    right++;
  }
}

4、回文串判断

1
2
3
4
5
6
7
8
9
10
11
boolean isPalindrome(String s){
    int left = 0, right = s.length() - 1;
    while(left < right){
        if (s.charAt(left) != s.charAt(right)){
            return false;
        }
        left++;
        right--;
    }
    return true;
}

难度提升：

  • [x] 5、最长回文子串

核⼼是从中⼼向两端扩散的双指针技巧

1
2
3
4
5
6
7
8
9
10
// 在 s 中寻找以 s[l] 和 s[r] 为中⼼的最⻓回⽂串, 如果输⼊相同的 l 和 r，就相当于寻找⻓度为奇数的回⽂串，如果输⼊相邻的 l 和 r，则相当于寻找⻓度为偶数的回⽂串
String palindrome(String s, int l, int r){
    //防止索引越界
    while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)){
        l--;
        r++;
    }
    //返回以s[l]和s[r]为中心的最长回文串
    return s.substring(l+1, r);
}

数组双指针经典高频题

  • 二分搜索

  • [x] 34、在排序数组中查找元素的第⼀个和最后⼀个位置

  • [x] 704、⼆分查找

  • [x] 剑指 Offer 53 - I. 在排序数组中查找数字 I

  • [x] 35、搜索插⼊位置

  • [x] 剑指 Offer II 068. 查找插⼊位置

  • [x] 240、搜索⼆维矩阵 II （从右上角遍历）

  • [x] 566、重塑矩阵

  • [x] 74、搜索⼆维矩阵

  • [ ] 剑指 Offer 04. ⼆维数组中的查找

  • [x] 519、随机翻转矩阵

  • [ ] 354、俄罗斯套娃信封问题

  • [ ] 392、判断⼦序列

  • [x] 658、找到 K 个最接近的元素

  • [ ] 793、阶乘函数后 K 个零

  • [ ] 852、⼭脉数组的峰顶索引

  • [ ] 剑指 Offer II 069. ⼭峰数组的顶部

  • [ ] 1011、在 D 天内送达包裹的能⼒

  • [ ] 875、爱吃⾹蕉的珂珂

  • [ ] 剑指 Offer II 073. 狒狒吃⾹蕉

  • [ ] 1201、丑数 III

  • [ ] 剑指 Offer 53 - II. 0～n-1中缺失的数字

滑动窗口

维护⼀个窗⼝，不断滑动，然后更新答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Void slidingWindow(String s) {
    HashMap<Character, Integer> window = new HashMap<>();
    int left = 0, right = 0;
    while(right < s.length()){
        // c 是将移入窗口的字符
        char c = s[right];
        // 增大窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...
        // 判断左侧窗口是否要收缩
        while(window needs shrink){
            // d 是将移出窗口的字符
            char d = s[left];
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

  • [x] 76、最小覆盖子串

  • [x] 567、字符串的排列

  • [x] 438、找到字符串中所有字母异位词

  • [x] 3、无重复字符的最长子串

二分查找详细

基本的二分搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

寻找左侧边界的二分搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int left_bound(int[] nums, int target) {
    int left = 0;
    int right = nums.length; // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

将其改写为搜索两端都封闭的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    // 此时 target 比所有数都大，返回 -1
    if (left == nums.length) return -1;
    // 判断一下 nums[left] 是不是 target
    return nums[left] == target ? left : -1;
}

寻找右侧边界的二分搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

将其改写为搜索两端都封闭的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 这里改成收缩左侧边界即可
            left = mid + 1;
        }
    }
    // 最后改成返回 left - 1
    if (left - 1 < 0) return -1;
    return nums[left - 1] == target ? (left - 1) : -1;
}

链表递归操作

1、递归反转链表

1
2
3
4
5
6
7
8
9
ListNode reverse(ListNode head){
    if(head == null || head.next == null){
        return head;
    }
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

2、反转链表前N个节点

1
2
3
4
5
6
7
8
9
10
11
ListNode successor = null;
ListNode reverseN(ListNode head, int n){
    if(n == 1){
        successor = head.next;
        return head;
    }
    ListNode last = reverseN(head.next, n-1);
    head.next.next = head;
    head.next = successor;
    return last;
}

3、反转链表的一部分

给定一个索引区间，仅仅反转区间中的链表元素

1
2
3
4
5
6
7
ListNode reverseBetween(ListNode head, int m, int n){
    if(m == 1){
        return reverseN(head, n);
    }
    head.next = reverseBetween(head.next, m-1, n-1);
    return head;
}
  • [x] 92、反转链表II

2、队列/栈

队列主要⽤在BFS算法，栈主要⽤在括号相关的问题

括号问题

1、判断有效括号串

  • [x] 20.有效的括号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public boolean isValid(String s) {
        Stack<Character> left = new Stack<>();
        for(char c : s.toCharArray()){
            if(c == '(' || c == '{' || c == '['){
                left.push(c);
            }
            else{
                if(!left.isEmpty() && leftOf(c) == left.peek()){
                    left.pop();
                }
                else return false;
            }
        }
        return left.isEmpty();
}
char leftOf(char c){
        if(c == '}')return '{';
        if(c == ')')return '(';
        return '[';
}

2、平衡括号串

  • [x] 921、使括号有效的最少添加
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int minAddToMakeValid(String s) {
        int res = 0;
        int need = 0;
        for(char c : s.toCharArray()){
            if(c == '('){
                need++;
            }
            else{
                need--;
                if(need == -1){
                    res++;
                    need = 0;
                }
            }
        }
        return res + need;
    }

进阶：现在假设1个左括号需要匹配2个右括号才叫做有效的括号组合

  • [x] 1541、平衡括号字符串的最少插入次数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int minInsertions(String s) {
        int res = 0, need = 0;
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                need += 2;
                if (need % 2 == 1) {
                    res++;
                    need--;
                }
            }
            if (s.charAt(i) == ')') {
                need--;
                if (need == -1) {
                    res++;
                    need = 1;
                }
            }
        }
        return res + need;
    }

单调栈

image-20230218214912678

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
int[] nextGreaterElement(int[] nums){
    int n = nums.length;
    int[] res = new int[n]; //存放答案的数组
    Stack<Integer> s = new Stack<>();
    for(int i = n - 1; i >= 0; i--){
        while(!s.isEmpty() && s.peek() <= nums[i]){
            s.pop();
        }
        res[i] = s.isEmpty() ? -1 : s.peek();
        s.push(nums[i]);
    }
    return res;
}

  • [x] 496.下一个更大元素I

  • [x] 739、每日温度

  • [x] 316、去除重复字母

环形数组

一般通过 % 运算符求模（余数），来模拟环形特效

1
2
3
4
5
6
int[] arr = {1, 2, 3, 4, 5};
int n = arr.length, index = 0;
while(true) {
    print(arr[index % n]);
    index++;
}
  • [x] 503.下一个更大元素II

通常还是调用单调栈模板，常用套路是将数组长度翻倍（可以不⽤构造新数组，⽽是利⽤循环数组的技巧来模拟数组⻓度翻倍的效果）

1
2
3
4
5
6
7
8
9
10
11
12
13
public int[] nextGreaterElements(int[] nums) {
        int n = nums.length;
        int[] res = new int[n];
        Stack<Integer> s = new Stack<>();
        for (int i = 2 * n - 1; i >= 0; i--) {
            while (!s.isEmpty() && s.peek() <= nums[i % n]) {
                s.pop();
            }
            res[i % n] = s.isEmpty() ? -1 : s.peek();
            s.push(nums[i % n]);
        }
        return res;
    }

单调队列

单调队列相比较优先级队列，除了能够维护最值，还能够维护队列元素的相对顺序。

  • [x] 239.滑动窗口最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class MonotonicQueue {
    LinkedList<Integer> maxq = new LinkedList<>();
    public void push(int n){
        // 将⼩于 n 的元素全部删除
        while(!maxq.isEmpty() && maxq.getLast() < n){
            maxq.pollPast();
        }
        // 然后将 n 加⼊尾部
        maxq.addLast(n);
    }
    
    public int max(){
        return maxq.getFirst();
    }
    
    public void pop(int n){
        if(n == maxq.getFirst()){
            maxq.pollFirst();
        }
    }
    // 之所以要判断 data.getFirst() == n，是因为想删除的队头元素 n 可能已经被「压扁」了，可能已 经不存在了，所以这时候就不⽤删除了
}

// 239 题解题
int[] maxSlidingWindow(int[] nums, int k) { 
    MonotonicQueue window = new MonotonicQueue();
    List<Integer> res = new ArrayList<>();
	for (int i = 0; i < nums.length; i++) { 
        if (i < k - 1) { 
            //先把窗⼝的前 k - 1 填满 
            window.push(nums[i]);
		} else { // 窗⼝开始向前滑动 // 移⼊新元素
			window.push(nums[i]); // 将当前窗⼝中的最⼤元素记⼊结果 
        	res.add(window.max()); // 移出最后的元素
			window.pop(nums[i - k + 1]); } 
    }
	// 将 List 类型转化成 int[] 数组作为返回值 
    int[] arr = new int[res.size()]; 
    for (int i = 0; i < res.size(); i++) { 
        arr[i] = res.get(i);
	} 
	return arr;
}

LRU算法

  • [x] 146、LRU缓存机制

LRU 算法设计

1、cache 中的元素必须有时序，以区分最近使⽤的和久未使⽤的数据，当容量满了之后要删除最久未使⽤的那个元素腾位置。

2、我们要在 cache 中快速找某个 key 是否已存在并得到对应的 val；
3、每次访问 cache 中的某个 key，需要将这个元素变为最近使⽤的，也就是说 cache 要⽀持在任意位置快速插⼊和删除元素。
那么，什么数据结构同时符合上述条件呢？哈希表查找快，但是数据⽆固定顺序；链表有顺序之分，插⼊删除快，但是查找慢。所以结合⼀下，形成⼀种新的数据结构：哈希链表 LinkedHashMap。

LRU 缓存算法的核⼼数据结构就是哈希链表，双向链表和哈希表的结合体。

image-20230220162529791

「为什么必须要⽤双向链表」：

删除⼀个节点不光要 得到该节点本身的指针，也需要操作其前驱节点的指针，⽽双向链表才能⽀持直接查找前驱，保证操作的时间复杂度 O(1)

注意我们实现的双链表 API 只能从尾部插⼊，也就是说靠尾部的数据是最近使⽤的，靠头部的数据是最久未使⽤的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class LRUCache {
    int cap;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();
    public LRUCache(int capacity){
        this.cap = capacity;
    }
    public int get(int key){
        if(!Cache.containKey(key)){
            return -1;
        }
        // 将key变为最近使用
        makeRecently(key);
        return cache.get(key);
    }
    
    public void put(int key, int val){
        if(cache.containsKey(key)){
            // 修改key的值
            cache.put(key, val);
            // 将key变为最近使用
            makeRecently(key);
            return;
        }
        if(cache.size() >= this.cap){
            // 链表头部就是最久未使⽤的 key
            int oldestKey = cache.keySet().iterator().next();
            // 将新的 key 添加链表尾部
            cache.remove(oldestKey)
        }
        cache.put(key, value);
    }
    
    private void makeRecently(int key){
        int val = cache.get(key);
        cache.remove(key);
        cache.put(key, val);
    }
}

二、进阶数据结构

1、二叉树思维

二叉树遍历框架

1
2
3
4
5
6
7
8
9
10
void traverse(TreeNode root){
    if(root == null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

⼆叉树题⽬的递归解法可以分两类思路，第⼀类是遍历⼀遍⼆叉树得出答案，第⼆类是通过分解问题计算出答案，这两类思路分别对应着 回溯算法核⼼框架 和 动态规划核⼼框架

  • [x] 104、二叉树的最大深度
一、翻转二叉树
1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode invertTree(TreeNode root) {
        traverse(root);
        return root;
}
void traverse(TreeNode root){
        if(root == null)return;
        traverse(root.left);
        traverse(root.right);
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
}
二、填充节点的右侧指针

题⽬的意思就是把⼆叉树的每⼀层节点都⽤ next 指针连接起来：

image-20230302163128694

1
2
3
4
5
6
7
8
9
10
11
12
public Node connect(Node root) {
        if(root == null)return null;
        traverse(root.left, root.right);
        return root;
}
void traverse(Node node1, Node node2){
        if(node1 == null && node2 == null)return;
        node1.next = node2;
        traverse(node1.left, node1.right);
        traverse(node2.left, node2.right);
        traverse(node1.right, node2.left);
}
三、将二叉树展开为链表

image-20230302165927112

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void flatten(TreeNode root) {
        if(root == null)return;
        flatten(root.left);
        flatten(root.right);
        TreeNode left = root.left;
        TreeNode right = root.right;
        root.left = null;
        root.right = left;
        TreeNode p = root;
        while(p.right != null){
            p = p.right;
        }
        p.right = right;
}

2、二叉树构造

image-20230303102820293

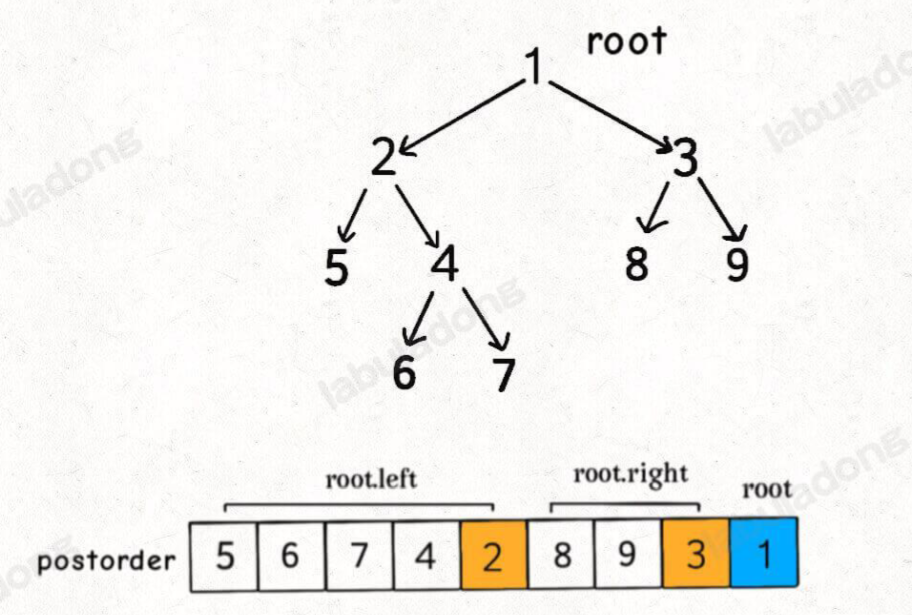
通过前序和中序遍历结果构造二叉树

image-20230303105456715

image-20230303105549467

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
HashMap<Integer, Integer> map = new HashMap<>();
   public TreeNode buildTree(int[] preorder, int[] inorder) {
       for (int i = 0; i < inorder.length; i++) {
           map.put(inorder[i], i);
       }
       return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
   }

   TreeNode build(int[] preorder, int prestart, int preend, int[] inorder, int instart, int inend) {
       if(prestart > preend)return null;
       int value = preorder[prestart];
       int index = map.get(value);
       TreeNode root = new TreeNode(value);
       int leftSize = index - instart;
       root.left = build(preorder, prestart + 1, prestart + leftSize, inorder, instart, index - 1);
       root.right = build(preorder, prestart + leftSize + 1, preend, inorder, index + 1, inend);
       return root;
   }
  • [x] 106、通过后序和中序遍历结果构造二叉树

3、序列化

  • [ ] 297、二叉树的序列化与反序列化

4、后序

  • [x] 652、寻找重复的子树

image-20230304100620430

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    HashMap<String, Integer> map = new HashMap<>();
    LinkedList<TreeNode> list = new LinkedList<TreeNode>();
    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        traverse(root);
        return list;
    }

    String traverse(TreeNode root){
        if(root==null)return "#";
        String left = traverse(root.left);
        String right = traverse(root.right);
        String subTree = left + ',' + right + ',' + root.val;

        int freq = map.getOrDefault(subTree, 0);
        if(freq == 1){
            list.add(root);
        }
        map.put(subTree, freq+1);
        return subTree;
    }
}

5、归并排序

归并排序的过程可以在逻辑上抽象成⼀棵⼆叉树，树上的每个节点的值可以认为是nums[lo…hi] ，叶⼦节点的值就是数组中的单个元素

image-20230306180234590

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Merge {

    // 用于辅助合并有序数组
    private static int[] temp;

    public static void sort(int[] nums) {
        // 先给辅助数组开辟内存空间
        temp = new int[nums.length];
        // 排序整个数组（原地修改）
        sort(nums, 0, nums.length - 1);
    }

    // 定义：将子数组 nums[lo..hi] 进行排序
    private static void sort(int[] nums, int lo, int hi) {
        if (lo == hi) {
            // 单个元素不用排序
            return;
        }
        // 这样写是为了防止溢出，效果等同于 (hi + lo) / 2
        int mid = lo + (hi - lo) / 2;
        // 先对左半部分数组 nums[lo..mid] 排序
        sort(nums, lo, mid);
        // 再对右半部分数组 nums[mid+1..hi] 排序
        sort(nums, mid + 1, hi);
        // 将两部分有序数组合并成一个有序数组
        merge(nums, lo, mid, hi);
    }

    // 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
    private static void merge(int[] nums, int lo, int mid, int hi) {
        // 先把 nums[lo..hi] 复制到辅助数组中
        // 以便合并后的结果能够直接存入 nums
        for (int i = lo; i <= hi; i++) {
            temp[i] = nums[i];
        }

        // 数组双指针技巧，合并两个有序数组
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
            if (i == mid + 1) {
                // 左半边数组已全部被合并
                nums[p] = temp[j++];
            } else if (j == hi + 1) {
                // 右半边数组已全部被合并
                nums[p] = temp[i++];
            } else if (temp[i] > temp[j]) {
                nums[p] = temp[j++];
            } else {
                nums[p] = temp[i++];
            }
        }
    }
}

  • [x] 315、计算右侧小于当前元素的个数
  • [x] 493、翻转对

6、二叉搜索树

BST特性：

1、对于 BST 的每⼀个节点 node，左⼦树节点的值都比 node 的值要小，右⼦树节点的值都比 node 的值大。
2、对于 BST 的每⼀个节点 node，它的左侧子树和右侧子树都是 BST。

BST 的中序遍历结果是有序的（升序）

  • [x] 230、二叉搜索树中第K小的元素

  • [x] 538、把二叉搜索树转换为累加树

基操

一、判断BST的合法性

  • [x] 98、验证二叉搜索树

二、在BST中插入一个数

1
2
3
4
5
6
7
8
9
10
11
TreeNode insertIntoBST(TreeNode root, int val) { 
	// 找到空位置插⼊新节点 
	if (root == null) return new TreeNode(val); 
    // if (root.val == val) 
    //	BST 中⼀般不会插⼊已存在元素 
    if (root.val < val) 
        root.right = insertIntoBST(root.right, val); 
    if (root.val > val) 
        root.left = insertIntoBST(root.left, val); 
    return root;
}

三、在BST中删除一个数

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode deleteNode(TreeNode root, int key) { 
    if (root.val == key) { 
        // 找到啦，进⾏删除
	} else if (root.val > key) { 
        // 去左⼦树找
	root.left = deleteNode(root.left, key);
	} else if (root.val < key) { 
        // 去右⼦树找
	root.right = deleteNode(root.right, key); 
    } 
    return root;
}

找到⽬标节点了，⽐⽅说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况

情况 1：A 恰好是末端节点，两个⼦节点都为空，那么它可以删除

情况 2：A 只有⼀个⾮空⼦节点，那么它要让这个孩⼦接替⾃⼰的位置。

image-20230313112836651

情况 3：A 有两个⼦节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左⼦树中最⼤的那个节点，或者右 ⼦树中最⼩的那个节点来接替⾃⼰。我们以第⼆种⽅式讲解

image-20230313112904170

1
2
3
4
5
6
7
if (root.left != null && root.right != null) { 
    // 找到右⼦树的最⼩节点
	TreeNode minNode = getMin(root.right); 
    // 把 root 改成 minNode root.val = minNode.val; 
    // 转⽽去删除 minNode
	root.right = deleteNode(root.right, minNode.val);
}

三种情况分析完毕，填⼊框架，简化⼀下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
TreeNode deleteNode(TreeNode root, int key) { 
    if (root == null) return null; 
    if (root.val == key) { 
        // 这两个 if 把情况 1 和 2 都正确处理了 
        if (root.left == null) return root.right; 
        if (root.right == null) return root.left; 
        // 处理情况 3 // 获得右⼦树最⼩的节点
		TreeNode minNode = getMin(root.right); // 删除右⼦树最⼩的节点
		root.right = deleteNode(root.right, minNode.val); // ⽤右⼦树最⼩的节点替换 root 节点 
        minNode.left = root.left; 
        minNode.right = root.right; 
        root = minNode;
	} else if (root.val > key) {
		root.left = deleteNode(root.left, key); 
    } else if (root.val < key) {
		root.right = deleteNode(root.right, key); 
    } 
    return root; 
}
	TreeNode getMin(TreeNode node) { // BST 最左边的就是最⼩的 
        while (node.left != null) node = node.left; 
        return node;
}

构造

  • [x] 96、不同的二叉搜索树

后序

  • [x] 1373、二叉搜索子树的最大键值和

7、快速排序

快速排序是先将一个元素排好序，然后再将剩下的元素排好序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Quick {

    public static void sort(int[] nums) {
        // 为了避免出现耗时的极端情况，先随机打乱
        shuffle(nums);
        // 排序整个数组（原地修改）
        sort(nums, 0, nums.length - 1);
    }

    private static void sort(int[] nums, int lo, int hi) {
        if (lo >= hi) {
            return;
        }
        // 对 nums[lo..hi] 进行切分
        // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
        int p = partition(nums, lo, hi);

        sort(nums, lo, p - 1);
        sort(nums, p + 1, hi);
    }

    // 对 nums[lo..hi] 进行切分
    private static int partition(int[] nums, int lo, int hi) {
        int pivot = nums[lo];
        // 关于区间的边界控制需格外小心，稍有不慎就会出错
        // 我这里把 i, j 定义为开区间，同时定义：
        // [lo, i) <= pivot；(j, hi] > pivot
        // 之后都要正确维护这个边界区间的定义
        int i = lo + 1, j = hi;
        // 当 i > j 时结束循环，以保证区间 [lo, hi] 都被覆盖
        while (i <= j) {
            while (i < hi && nums[i] <= pivot) {
                i++;
                // 此 while 结束时恰好 nums[i] > pivot
            }
            while (j > lo && nums[j] > pivot) {
                j--;
                // 此 while 结束时恰好 nums[j] <= pivot
            }
            // 此时 [lo, i) <= pivot && (j, hi] > pivot

            if (i >= j) {
                break;
            }
            swap(nums, i, j);
        }
        // 将 pivot 放到合适的位置，即 pivot 左边元素较小，右边元素较大
        swap(nums, lo, j);
        return j;
    }

    // 洗牌算法，将输入的数组随机打乱
    private static void shuffle(int[] nums) {
        Random rand = new Random();
        int n = nums.length;
        for (int i = 0 ; i < n; i++) {
            // 生成 [i, n - 1] 的随机数
            int r = i + rand.nextInt(n - i);
            swap(nums, i, r);
        }
    }

    // 原地交换数组中的两个元素
    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

变体：快速选择

  • [x] 215、数组中的第K个最大元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int findKthLargest(int[] nums, int k) {
    // 首先随机打乱数组
    shuffle(nums);
    int lo = 0, hi = nums.length - 1;
    // 转化成「排名第 k 的元素」
    k = nums.length - k;
    while (lo <= hi) {
        // 在 nums[lo..hi] 中选一个分界点
        int p = partition(nums, lo, hi);
        if (p < k) {
            // 第 k 大的元素在 nums[p+1..hi] 中
            lo = p + 1;
        } else if (p > k) {
            // 第 k 大的元素在 nums[lo..p-1] 中
            hi = p - 1;
        } else {
            // 找到第 k 大元素
            return nums[p];
        }
    }
    return -1;
}


// 对 nums[lo..hi] 进行切分
int partition(int[] nums, int lo, int hi) {
    // 见前文
}

// 洗牌算法，将输入的数组随机打乱
void shuffle(int[] nums) {
    // 见前文
}

// 原地交换数组中的两个元素
void swap(int[] nums, int i, int j) {
    // 见前文
}

8、图

图本质上就是个⾼级点的多叉树，适⽤于树的 DFS/BFS 遍历算法，全部适用于图。

常用邻接表和邻接矩阵来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 记录被遍历过的节点 boolean[] visited; 
// 记录从起点到当前节点的路径 boolean[] onPath;
/* 图遍历框架 */ 
void traverse(Graph graph, int s) { 
    if (visited[s]) 
        return; 
    // 经过节点 s，标记为已遍历 
    visited[s] = true; 
    // 做选择：标记节点 s 在路径上 
    onPath[s] = true; 
    for (int neighbor : graph.neighbors(s)) { 
        traverse(graph, neighbor);
	}
// 撤销选择：节点 s 离开路径 onPath[s] = false;
}
  • [x] 797、所有可能路径

9、拓扑排序

两个图论算法：有向图的环检测、拓扑排序算法

环检测算法（DFS 版本）
  • [x] 207、课程表

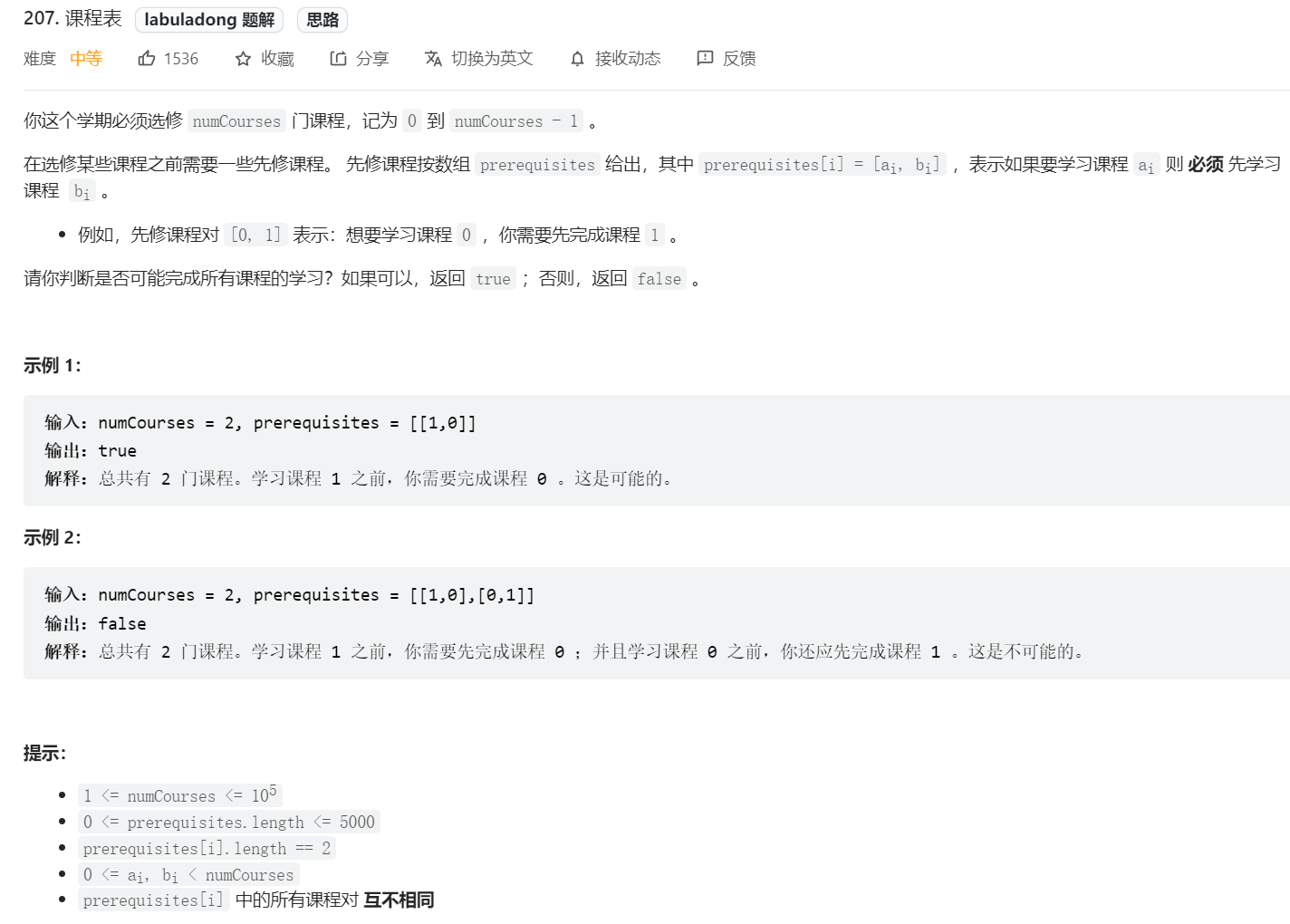
image-20230319170253160

⾸先就是把问题转化成「有向图」这种数据结构，只要图中存在环，那就说明存在循 环依赖

如果发现有向图中存在环，那就说明课程之间存在循环依赖，肯定没办法全部上完；反之，如果没有 环，那么肯定能上完全部课程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
    // 记录一次 traverse 递归经过的节点
    boolean[] onPath;
    // 记录遍历过的节点，防止走回头路
    boolean[] visited;
    // 记录图中是否有环
    boolean hasCycle = false;

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = buildGraph(numCourses, prerequisites);

        visited = new boolean[numCourses];
        onPath = new boolean[numCourses];

        for (int i = 0; i < numCourses; i++) {
            // 遍历图中的所有节点
            traverse(graph, i);
        }
        // 只要没有循环依赖可以完成所有课程
        return !hasCycle;
    }

    void traverse(List<Integer>[] graph, int s) {
        if (onPath[s]) {
            // 出现环
            hasCycle = true;
        }

        if (visited[s] || hasCycle) {
            // 如果已经找到了环，也不用再遍历了
            return;
        }
        // 前序遍历代码位置
        visited[s] = true;
        onPath[s] = true;
        for (int t : graph[s]) {
            traverse(graph, t);
        }
        // 后序遍历代码位置
        onPath[s] = false;
    }

    List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
        // 图中共有 numCourses 个节点
        List<Integer>[] graph = new LinkedList[numCourses];
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new LinkedList<>();
        }
        for (int[] edge : prerequisites) {
            int from = edge[1];
            int to = edge[0];
            // 修完课程 from 才能修课程 to
            // 在图中添加一条从 from 指向 to 的有向边
            graph[from].add(to);
        }
        return graph;
    }
}

PS：类⽐贪吃蛇游戏，visited 记录蛇经过过的格⼦，⽽ onPath 仅仅记录蛇身。onPath ⽤于判断 是否成环，类⽐当贪吃蛇⾃⼰咬到⾃⼰（成环）的场景。

拓扑排序
  • [x] 210、课程表II

image-20230319170702569

如果把课程抽象成节点，课程之间的依赖关系抽象成有向边，那么这幅图的拓扑排序结果就是上课顺序

先判断⼀下题⽬输⼊的课程依赖是否成环，成环的话是⽆法进⾏拓扑排序的。将后序遍历的结果进⾏反转，就是拓扑排序的结果。

image-20230319184241791

210题代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    boolean flag = false;
    boolean[] visit;
    boolean[] onPath;
    List<Integer> preorder = new LinkedList<>();
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        List<Integer>[] path = new LinkedList[numCourses];
        visit = new boolean[numCourses];
        onPath = new boolean[numCourses];
        for(int i = 0; i < numCourses; i++){
            path[i] = new LinkedList<Integer>();
        }
        for(int[] j : prerequisites){
            path[j[1]].add(j[0]);
        }
        for(int i = 0; i < numCourses; i++){
            traverse(path, i);
        }
        if(flag)return new int[]{};
        Collections.reverse(preorder);
        int[] res = new int[numCourses];
        for(int i = 0; i < preorder.size(); i++){
            res[i] = preorder.get(i);
        }
        return res;
    }
    public void traverse(List<Integer>[] path, int s){
        if(onPath[s]){
            flag = true;
        }
        if(flag || visit[s])return;
        visit[s] = true;
        onPath[s] = true;
        for(int j : path[s]){
            traverse(path, j);
        }
        preorder.add(s);
        onPath[s] = false;
    }
}
环检测算法（BFS 版本）

思路：

1、构建邻接表，和之前⼀样，边的⽅向表示「被依赖」关系。

2、构建⼀个 indegree 数组记录每个节点的⼊度，即 indegree[i] 记录节点 i 的⼊度。

3、对 BFS 队列进⾏初始化，将⼊度为 0 的节点⾸先装⼊队列。

4、开始执⾏ BFS 循环，不断弹出队列中的节点，减少相邻节点的⼊度，并将⼊度变为 0 的节点加⼊队列。

5、如果最终所有节点都被遍历过（count 等于节点数），则说明不存在环，反之则说明存在环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public boolean canFinish(int numCourses, int[][] prerequisites) { 
    // 建图，有向边代表「被依赖」关系
List<Integer>[] graph = buildGraph(numCourses, prerequisites); // 构建⼊度数组 
    int[] indegree = new int[numCourses]; 
    for (int[] edge : prerequisites) { 
        int from = edge[1], to = edge[0]; 
        // 节点 to 的⼊度加⼀ 
        indegree[to]++;
	}
	// 根据⼊度初始化队列中的节点 
    Queue<Integer> q = new LinkedList<>(); 
    for (int i = 0; i < numCourses; i++) { 
        if (indegree[i] == 0) { 
            // 节点 i 没有⼊度，即没有依赖的节点 
            // 可以作为拓扑排序的起点，加⼊队列 
            q.offer(i);
		} 
    }
	// 记录遍历的节点个数 
    int count = 0; 
    // 开始执⾏ BFS 循环 
    while (!q.isEmpty()) { 
        // 弹出节点 cur，并将它指向的节点的⼊度减⼀ 
        int cur = q.poll(); count++; 
        for (int next : graph[cur]) { 
            indegree[next]--; 
            if (indegree[next] == 0) { 
                // 如果⼊度变为 0，说明 next 依赖的节点都已被遍历
                q.offer(next);
			} 
        } 
    }
	// 如果所有节点都被遍历过，说明不成环 
    return count == numCourses;
}
#算法
算法基础
http://willimt.com/2023/02/15/lt/leetcode算法/
作者
Willimt
发布于
2023年2月15日
许可协议